در هندسه، یک اَبَرمکعب، یک چند-بعدی پیوسته از یک مربع (۲=n) و یک مکعب (۳=n)است. فوق مکعب، یک شکل محدب فشرده بسته، است که از یک ساختار متشکل از گروه پارهخطهای موازی متقابل، در هریک از ابعاد فضا، با زاویههای عمود بر یکدیگر و طول یکسان تشکیل شدهاست.
یک اَبَرمکعب چند بُعدی با نام چندمکعب (n-cube) نیز نامیده میشود. از اصطلاح«measure polytope» نیز معمولاً استفاده میشود، به طور مشخص در عمل، هارولد اسکات مکدونالد کوکسِتر (H.S.M. Coxeter)از این اصطلاح استفاده کردهاست که اکنون این واژه کنار گذاشته میشود. یک ابرمکعب حالت خاصی از اَبَر مکعبمستطیل است، که با نام ارتوتوپ(orthotope) نیز نامیده میشود. یک ابرمکعب یکه (واحد)، یک فوقمکعب با طول ضلع ۱ است. اغلب در فضای nبعدی  ، گوشهها یا رأسهای فوقمکعب واحد تعداد
، گوشهها یا رأسهای فوقمکعب واحد تعداد  نقطه، با مختصات ۰ یا ۱ است.
نقطه، با مختصات ۰ یا ۱ است.
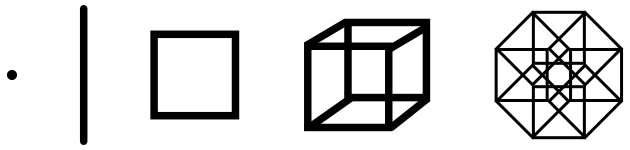 نقطه به عنوان ابرمکعب [ویرایش]
نقطه به عنوان ابرمکعب [ویرایش]
یک نقطه، یک اَبَرمکعب با بعد صفر است. یعنی نقطه را میتوان نوعی فوقمکعب در فضای  نامید. اگر این نقطه به اندازهٔ یک واحد به سمتی، حرکت کند، یک پارهخط پدید میآورد. یا به اصطلاح، مسیری را که طی میکند یک پارهخط است. پارهخط یک اَبرمکعب با بعد یک است. به بیان دیگر، پارهخط نوعی فوقمکعب در فضای
نامید. اگر این نقطه به اندازهٔ یک واحد به سمتی، حرکت کند، یک پارهخط پدید میآورد. یا به اصطلاح، مسیری را که طی میکند یک پارهخط است. پارهخط یک اَبرمکعب با بعد یک است. به بیان دیگر، پارهخط نوعی فوقمکعب در فضای  است.
است.
اگر این پارهخط در امتدادی عمود بر طول خودش، به اندازه یک واحد جابجا شود، سطحی دوبعدی به شکل مربع پدید میآورد. این مربع، یک ابرمکعب در فضای  خواهد بود. به همین ترتیب، اگر مربع را به اندازهٔ یک واحد، در راستای عمود بر سطح خودش، جابجا کنیم، یک مکعب سهبعدی پدید خواهد آمد (ابرمکعبی در فضای ریاضی
خواهد بود. به همین ترتیب، اگر مربع را به اندازهٔ یک واحد، در راستای عمود بر سطح خودش، جابجا کنیم، یک مکعب سهبعدی پدید خواهد آمد (ابرمکعبی در فضای ریاضی 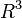 ). این شیوه در باره فضای چندبعدی، و دستیابی به ابرمکعبهای nبعدی نیز قابل گسترش است. برای مثال، اگر یک مکعب ۳بعدی را در راستای بُعد چهارمش به اندازهٔ یک واحد، جابجا کنیم، یک ابرمکعب ۴بعدی با ابعاد واحد بهدست خواهد آمد.
). این شیوه در باره فضای چندبعدی، و دستیابی به ابرمکعبهای nبعدی نیز قابل گسترش است. برای مثال، اگر یک مکعب ۳بعدی را در راستای بُعد چهارمش به اندازهٔ یک واحد، جابجا کنیم، یک ابرمکعب ۴بعدی با ابعاد واحد بهدست خواهد آمد.
این فرآیند حرکت بر امتداد عمود بر شیء، میتواند به شیوهٔ ریاضی با جمع مینکوفسکی بیان شود.
ابرمکعب dبعدی، یک جمع مینکوفسکی از پارهخطهای دوبدو متعامد شکل گرفته و در نتیجه یک مثال از زونوتوپ است.
از دیدگاه ریختشناسی (توپولوژی) ساختار تک-اسکلتی ابرمکعب یک گراف ابرمکعب است.
یک ابرمکعب یکهٔ چندبعدی، یک سطح محدب از نقاط با دگرگونیهای علامت در مختصات کارتزین است 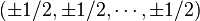 . طول هر ضلع آن برابر ۱ و حجمش نیز ۱ واحد است.
. طول هر ضلع آن برابر ۱ و حجمش نیز ۱ واحد است.
همچنین یک ابرمکعب n-بعدی اغلب به عنوان رویهٔ محدب تلقی شدهاست 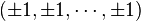 . اغلب این فرم بهخاطر سهولت در نوشتن مختصات انتخاب شدهاست. طول لبهٔ آن ۲ است و رتبه n-بعدیاش نیز ۲ است (
. اغلب این فرم بهخاطر سهولت در نوشتن مختصات انتخاب شدهاست. طول لبهٔ آن ۲ است و رتبه n-بعدیاش نیز ۲ است ( ).
).
نظرات شما عزیزان:

 ، گوشهها یا رأسهای فوقمکعب واحد تعداد
، گوشهها یا رأسهای فوقمکعب واحد تعداد  نقطه، با مختصات ۰ یا ۱ است.
نقطه، با مختصات ۰ یا ۱ است.
 نامید. اگر این نقطه به اندازهٔ یک واحد به سمتی، حرکت کند، یک پارهخط پدید میآورد. یا به اصطلاح، مسیری را که طی میکند یک پارهخط است. پارهخط یک اَبرمکعب با بعد یک است. به بیان دیگر، پارهخط نوعی فوقمکعب در فضای
نامید. اگر این نقطه به اندازهٔ یک واحد به سمتی، حرکت کند، یک پارهخط پدید میآورد. یا به اصطلاح، مسیری را که طی میکند یک پارهخط است. پارهخط یک اَبرمکعب با بعد یک است. به بیان دیگر، پارهخط نوعی فوقمکعب در فضای  است.
است. خواهد بود. به همین ترتیب، اگر مربع را به اندازهٔ یک واحد، در راستای عمود بر سطح خودش، جابجا کنیم، یک مکعب سهبعدی پدید خواهد آمد (ابرمکعبی در فضای ریاضی
خواهد بود. به همین ترتیب، اگر مربع را به اندازهٔ یک واحد، در راستای عمود بر سطح خودش، جابجا کنیم، یک مکعب سهبعدی پدید خواهد آمد (ابرمکعبی در فضای ریاضی 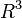 ). این شیوه در باره فضای چندبعدی، و دستیابی به ابرمکعبهای nبعدی نیز قابل گسترش است. برای مثال، اگر یک مکعب ۳بعدی را در راستای بُعد چهارمش به اندازهٔ یک واحد، جابجا کنیم، یک ابرمکعب ۴بعدی با ابعاد واحد بهدست خواهد آمد.
). این شیوه در باره فضای چندبعدی، و دستیابی به ابرمکعبهای nبعدی نیز قابل گسترش است. برای مثال، اگر یک مکعب ۳بعدی را در راستای بُعد چهارمش به اندازهٔ یک واحد، جابجا کنیم، یک ابرمکعب ۴بعدی با ابعاد واحد بهدست خواهد آمد.
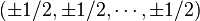 . طول هر ضلع آن برابر ۱ و حجمش نیز ۱ واحد است.
. طول هر ضلع آن برابر ۱ و حجمش نیز ۱ واحد است.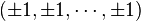 . اغلب این فرم بهخاطر سهولت در نوشتن مختصات انتخاب شدهاست. طول لبهٔ آن ۲ است و رتبه n-بعدیاش نیز ۲ است (
. اغلب این فرم بهخاطر سهولت در نوشتن مختصات انتخاب شدهاست. طول لبهٔ آن ۲ است و رتبه n-بعدیاش نیز ۲ است ( ).
).